新课标的一个重要课程目标是利用数学知识解决生活中的实际问题，是学生学习知识、形成技能和发展为能力的结果，也是学生具备了建模思想的重要标志。

　　构建数学模型解决实际问题基本步骤如下：

　　1、阅读、审题：

　　要做到简缩问题，删掉次要语句，深入理解关键字句；为便于数据处理，最好运用表格（或图形）处理数据，便于寻找数量关系。

　　2、建模、建立数学关系式：

　　将问题简单化、符号化，尽量借鉴标准形式，建立数学关系式。

　　3、运用数学知识

　　4、解释并回答实际问题

　　为了更加形象表示，我们可以参考下面的图标：

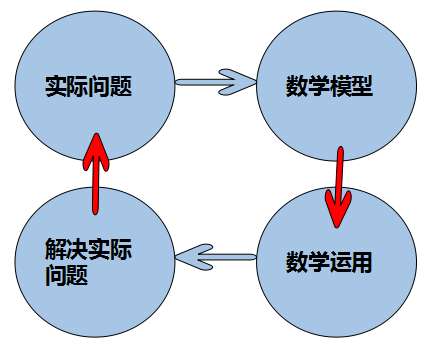
　　那么一起来看看数学和生活实际问题在中考中是怎么体现：

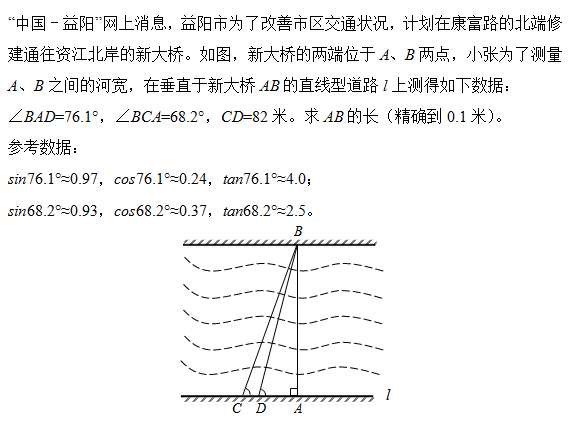
　　一、方程模型的应用

　　基本步骤：设元、列方程、解方程。解应用题的关键是：寻找题目中的等量关系，尤其是从语言中挖掘等量关系。找等量关系实际上就是从实际问题到建立数学模型的一个过渡阶段。

　　下面以2014年益阳的第18题为例：

　　二、方程不等式模型的综合应用

　　在解决方案型问题时，可由方程模型建立多个未知数之间的关系，最终通过代换消元，得到不等式中的整数解，进而得出几种方案。

　　下面以2014年贵州黔东南州第23题为例：

　　某超市计划购进一批甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元。

　　（1）求每件甲种、乙种玩具的进价分别是多少元？

　　（2）如果购进甲种玩具有优惠，优惠方法是：购进甲种玩具超过20件，超出部分可以享受7折优惠，若购进x（x＞0）件甲种玩具需要花费y元，请你求出y与x的函数关系式；

　　（3）在（2）的条件下，超市决定在甲、乙两种玩具中选购其中一种，且数量超过20件，请你帮助超市判断购进哪种玩具省钱。

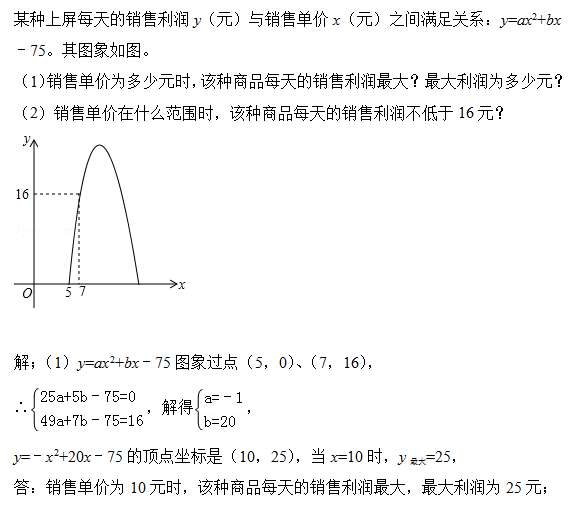
　　三、函数模型在最值问题中的应用

　　在最值问题中，如果题中没有设出自变量，最后让求最值时，可分析题中哪个量引起另一个的变化，可设这两个量分别为自变量和函数，建立函数关系式，注意自变量的范围，如果是一次函数的最值问题，一定要求自变量的取值范围，结合一次函数的增减性求最值；如果是二次函数的最值问题，利用配方法后，一定要看顶点横坐标是否在自变量的范围内，若不在，结合图像求解。

　　下面以2014年江苏徐州的第26题为例：

　　四、几何模型的应用

　　构建几何模型就是把实际问题中本质的东西抽象为几何图形（线段、直角三角形，等腰三角形、平行四边形、梯形等），利用几何图形的性质解决实际问题。

　　下面以2014年浙江宁波的第26题为例：